LaTeX 的 Markdown 语法
- 上下标: 上标 ^ 下标 _
- 分式: \frac{分子}{分母}
- 分式单个:\frac 分子 分母
- 根式: \sqrt 默认是平方根 \sqrt[ 根的次数]{数值}
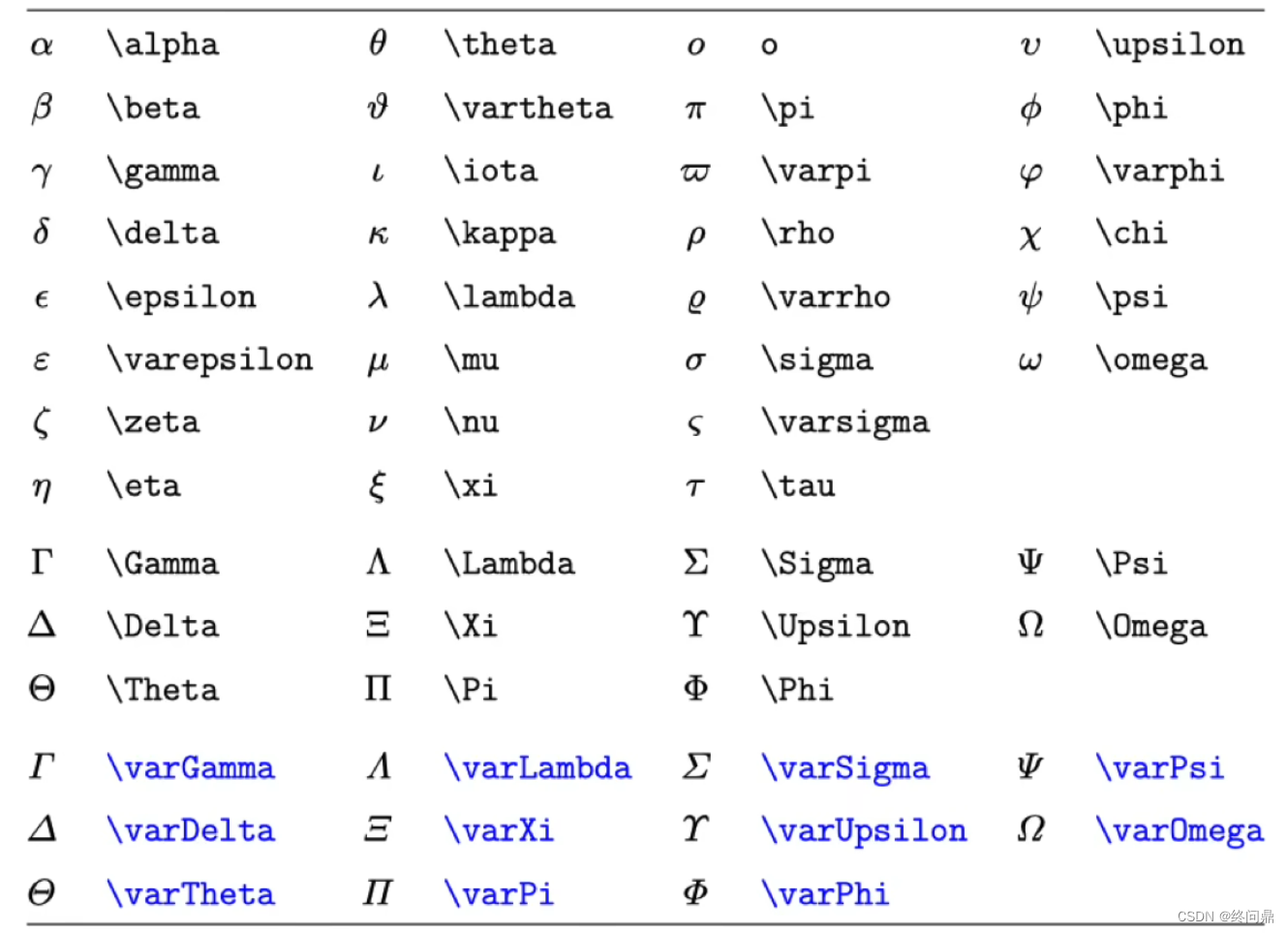
希腊字母
大写的首字母将全拼首字母大写即可。
运算符
- 加,减,正负,负正,乘,点乘,除
+. -, $\pm$, $\mp$, $\times$, $\cdot$, $\div$
+. -, $\pm$, $\mp$, $\times$, $\cdot$, $\div$
- 大小于,大于等于,小于等于,远大于,远小于,不等于,约等于,恒等于
$>$, $<$, $\ge$, $\le$, $\gg$, $\ll$, $\ne$, $\approx$, $\equiv$
$>$, $<$, $\ge$, $\le$, $\gg$, $\ll$, $\ne$, $\approx$, $\equiv$
- 交集,并集,属于,不属于,子集,真子集,空集
$\cap$, $\cup$, $\in$, $\notin$, $\subseteq$, $\subsetneqq$, $\varnothing$
$\cap$, $\cup$, $\in$, $\notin$, $\subseteq$, $\subsetneqq$, $\varnothing$
- 对任意,存在,不存在, 因为,所以
$\forall$, $\exists$, $\nexists$, $\because$, $\therefore$
$\forall$, $\exists$, $\nexists$, $\because$, $\therefore$
- 实数集,有理数集,自然数,整数集, 正整数集
$\ R$, $\ Q$, $\ N$, $\ Z$, $\Z_+$
$\ R$, $\ Q$, $\ N$, $\ Z$, $\Z_+$
- 傅里叶,花体傅里叶, 横向省略号,竖向省略号,斜向省略号
$\mathcal F$, $\mathscr F$, $\cdots$, $\vdots$, $\ddots$
$\mathcal F$, $\mathscr F$, $\cdots$, $\vdots$, $\ddots$
- 无穷,偏微分,梯度算子,正比于,度
$\infty$, $\partial$, $\nabla$, $\propto$, $\degree$
$\infty$, $\partial$, $\nabla$, $\propto$, $\degree$
- 三角函数, 对数
$\sin x$, $\sec x$, $\cosh x$, $\log_2 x$, $\ln n$
$\sin x$, $\sec x$, $\cosh x$, $\log_2 x$, $\ln n$
- 趋于,极限,强制位置(极限位置强制到下方)
$\to0$, $\lim_{x \to0}$, $\lim\limits_{x \to0}$
$\to0$, $\lim_{x \to0}$, $\lim\limits_{x \to0}$
大型运算符
- 求和,求积,积分,多重积分,回路积分,双重回路积分
$\sum$, $\prod$, $\int$, $\iint$, $\iiint$,$\oint$,$\oiint$
$\sum$, $\prod$, $\int$, $\iint$, $\iiint$,$\oint$,$\oiint$
一个例子:中间的,表示空格
$\int_{-\infty}^0 f(x)\, \text d x$
$\int_{-\infty}^0 f(x)\, \text d x$
- 空格
$a a$
$a\ a$
$a\quad a$
$a\qquad a$
$a a$
$a\ a$
$a\quad a$
$a\qquad a$
向量集合
\surd \sqrt{2} \sqrt[n]{n} \sqrt[n]{x+y}
\{ \} \in \emptyset \not\in \not\ni \ni \cup \cap \supset \subset \nsubseteq \subseteq \nsupseteq \supseteq
\overline{AB} \overleftarrow{AB} \overrightarrow{AB} \underline{AB}
\check{a} \tilde{a} \acute{a} \grave{a} \breve{a} \bar{a} \vec{a} \mathring{a} \dot{a} \ddot{a} \hat{a}
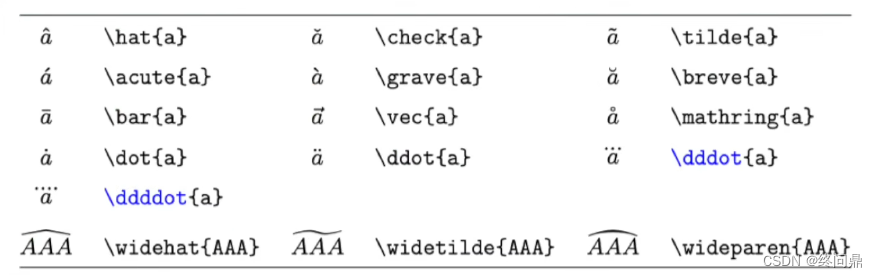
标注符号
单字符向量(固定长度箭头短),多字符向量(箭头长度随着字符数量的增多变化),单均值,多字符均值
箭头

括号,定界符
大括号,左侧上取整,右侧上取整,左侧下取整,右侧下取整,绝对值
$\{ \}$, $\lceil$, $\rceil$, $\lfloor$, $\rfloor$, $| |$
| ${ }$, $\lceil$, $\rceil$, $\lfloor$, $\rfloor$, $ | $ |
多行公式
多行环境:\代表换行,默认右对其,可以在等号前加&实现等号对齐,具体是&后一对齐
$$\begin{align}
a+b=c\\a+f=d\\cd=ef
\end{align}$$
大括号,条件表达
$$f(x)=
\begin{cases}
\sin x, -1\le x\le2\\
\cos x, else
\end{cases}$$
此外还有单纯的括号加大:
$$
\left(a\right), \big(a\big) , \Big(a\Big), \bigg(a\bigg), \Bigg(a\Bigg)
$$
矩阵
- 转置
$$ \bf B^T $$
- 无括号
$$
\begin{matrix}
a & b&c&\cdots&d\\
\vdots & \vdots & \vdots & \ddots &\vdots \\
e & k & f & \cdots & 0
\end{matrix}
$$
- 方括号
$$
\begin{bmatrix}
a & b&c&\cdots&d\\
\vdots & \vdots & \vdots & \ddots &\vdots \\
e & k & f & \cdots & 0
\end{bmatrix}
$$
- 圆形括号
$$
\begin{pmatrix}
a & b&c&\cdots&d\\
\vdots & \vdots & \vdots & \ddots &\vdots \\
e & k & f & \cdots & 0
\end{pmatrix}
$$
- 行列式写法
$$
\begin{vmatrix}
a & b&c&\cdots&d\\
\vdots & \vdots & \vdots & \ddots &\vdots \\
e & k & f & \cdots & 0
\end{vmatrix}
$$